The Pew Research Center released a report today about economic segregation (complete pdf report) in the United States, authored by Paul Taylor and Richard Fry. It is an interesting and well done policy piece that summarizes its findings as follows.
Residential segregation by income has increased during the past three decades across the United States and in 27 of the nation’s 30 largest major metropolitan areas.
In this post, I will describe briefly how the numbers reported in that report were calculated and then point out a potential difficulty with their interpretation.
1. Measuring economic segregation. The Pew analysis divides all households into three income brackets,
- “Lower Income”: household income is less than two-thirds of the national median annual income (<$34,000),
- “Upper Income: household income is greater than double the national median annual income (>$104,000), and
- “Middle Income”: household income is greater than two-thirds of the national median annual income and less than double the national median annual income (between $34,000 and $104,000).
Then, Pew counted the number of each type of household in each tract. If in any tract over half the households were lower income, then the tract was classified as a “Majority Lower Income Tract.” Similarly, if in any tract over half the households were upper income, then the tract was classified as a “Majority Upper Income Tract.” For each city, Pew then calculated
- the percentage of lower income households that were in Majority Lower Income Tracts and
- the percentage of upper income households that were in Majority Upper Income Tracts.
Finally, Pew added these two percentages together and multiplied the sum by 100. The result is a scale that ranges from 0 to 200: 0 means that no lower (or upper) income households in the city were located in majority lower income tracts (or, respectively, majority upper income tracts) while 200 means that every lower (and upper) income household in the city was located in a majority lower income tract (respectively, majority upper income tract).
It’s a complicated measure, which I will now simply call the segregation score, but I see its appeal. If it is unclear, the relevant point is that higher values of the measure imply that a randomly chosen lower or upper income household is more likely to have neighbors with similar household incomes.
Before continuing, note a couple of things:
- I like the measure in many ways (for example, it’s actually measuring something about households rather than only about neighborhoods). Of course, that does not mean I think it is the best way to measure segregation (income/economic or otherwise)—but I think there is no unambiguously “best” measure of this, as any such measure is an aggregation function.
- A higher score on this measure does not necessarily imply that a randomly chosen upper income household is likely to have fewer lower income neighbors. This is because the measure does not capture the full distribution of incomes in a number of ways. As the point above alludes to, this is not something to fault the authors on.
2. Not Your Daddy’s Census Tract. The difficulty I want to describe is a matter of measurement. The authors understandably want to talk about neighborhoods and spatial segregation. Measuring neighborhoods is hard. In particular, and as the authors describe (fn. 2),
The nation’s 73,000 census tracts are the best statistical proxy available from the Census Bureau to define neighborhoods. … As a general rule, a census tract conforms to what people typically think of as a neighborhood.
I agree wholeheartedly with the authors on this point. However, defining a neighborhood at any one point in time is not the same as defining that neighborhood so that it is comparable across time.
Digression qua True Story. My mother’s family used to give directions with respect to a well-known “dirt pile” owned by their county. Years passed and the dirt, well, went somewhere. Around that time, her family started giving (and I think still gives) directions with respect to “where that dirt pile used to be.”
In a nutshell, the authors want to compare neighborhoods across about 30 years. In terms of their segregation measure described above, they need to choose a set of census tracts as the comparison set. In particular, there are a few good reasons to choose a given set of census tracts and create the segregation measure for each city in 1980 and in 2010 using that same set of census tracts.
The definition of census tracts is described in this document. In a nutshell, census tracts are
…small, relatively permanent geographic entities within counties (or the statistical equivalents of counties) delineated by a committee of local data users. Generally, census tracts have between 2,500 and 8,000 residents and boundaries that follow visible features. When first established, census tracts are to be as homogeneous as possible with respect to population characteristics, economic status, and living conditions.
(Emphasis added. And emphasized again in part.)
The highlighted part of this description indicates the difficulty. In particular, the Pew analysis is quite (admirably) clear in their construction of the data: to compare the same neighborhoods between 1980 and 2010, they used census tracts from the 2000 census.
Note: The authors had to choose between 2000 and 2010, as census tracts became universal only in the 2000 census.
So, what does this mean? Well, the census lines in question were drawn in 2000 with one of the goals being the maximization of homogeneity of economic status. Thus, it is unsurprising that one finds greater economic homogeneity within census tracts between 2006 and 2010 than one finds in those same census tracts in 1980. This is a convoluted version of “regression to the mean.” In particular, if you create groupings so as to maximize some time-varying statistic (here, economic/income homogeneity), then many of the groupings will have (possibly very far) above average values of that statistic at the time of their creation. Accordingly, they will tend to have lower levels of that statistic at any time other than when they are created.
Whew….put in the context of the segregation score analysis under discussion:
More economically homogeneous census tracts will generally lead to higher segregation scores as computed in the Pew report.
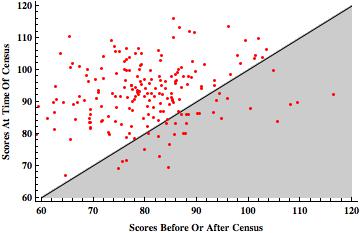
I programmed and ran a simple Monte Carlo experiment to demonstrate this. I am happy to share the code and details with interested readers. (Simply email me.) In a nutshell, I ran 200 simulations and in 169 of them, the segregation scores from what the “census year” (i.e., when tracts were drawn) were higher than the same scores from the non-census year (i.e., when incomes vary but tracts do not). The results are displayed visually below.
One point that is key in thinking about the simulation results is that the income distributions in the two time periods were independently drawn. This is unrealistic, but it presents most clearly and accurately the effect of the “regression to the mean” artifact introduced by the asymmetric timing of tract drawing.
[Visually, every dot in the white “upper left” part of the graph indicates a simulation where the score indicated increasing segregation, as found in the Pew report, and every dot in gray “lower right” part indicate the reverse. Since the incomes are actually (by construction) unrelated in the simulations, one should expect—if the timing of the construction of census tracts doesn’t matter—that about half of the dots to be in each of the two areas.]
The main point here is more than that it is difficult to make an apples-to-apples comparison of neighborhoods over time—rather, from the “math of politics” angle, the key point is as follows:
The use of census tracts drawn in 2000 so as to accentuate intra-tract economic heterogeneity to compare income segregation in 1980 and the early 21st century biases the measure in favor of finding an increase in income segregation.
Before concluding, I want to make clear that I am not asserting (nor do I believe) that the conclusions of the Pew report are incorrect. I am simply pointing out a difficulty with the construction of the data and, hence, the authors’ measure of change in segregation at a neighborhood level. Note that the difficulty I highlight would not apply if census tracts were drawn independently of the local distribution of economic statuses. Finally, it is also worth noting that the above-cited Census Bureau document points out the dilemma facing the Pew analysis:
The Census Bureau also requests that at the time each census tract is established, it contain (if possible) a population whose housing and socioeconomic characteristics are similar. Because the characteristics of neighborhoods and other small areas change with time, census tracts may become less homogeneous in succeeding censuses.
I guess an implication of my argument here is that the conclusion of the final sentence could be applied to preceding censuses as well.
In conclusion, I leave you with this.