Author Archives: admin

Keeping Tract: Is Income Segregation Getting Worse in the US?

Posted on by

The Pew Research Center released a report today about economic segregation (complete pdf report) in the United States, authored by Paul Taylor and Richard Fry.  It is an interesting and well done policy piece that summarizes its findings as follows.

Residential segregation by income has increased during the past three decades across the United States and in 27 of the nation’s 30 largest major metropolitan areas.

In this post, I will describe briefly how the numbers reported in that report were calculated and then point out a potential difficulty with their interpretation.

1. Measuring economic segregation. The Pew analysis divides all households into three income brackets,

  1. “Lower Income”: household income is less than two-thirds of the national median annual income (<$34,000),
  2. “Upper Income: household income is greater than double the national median annual income (>$104,000), and
  3. “Middle Income”: household income is greater than two-thirds of the national median annual income and less than double the national median annual income (between $34,000 and $104,000).

Then, Pew counted the number of each type of household in each tract.  If in any tract over half the households were lower income, then the tract was classified as a “Majority Lower Income Tract.” Similarly, if in any tract over half the households were upper income, then the tract was classified as a “Majority Upper Income Tract.” For each city, Pew then calculated

  1. the percentage of lower income households that were in Majority Lower Income Tracts and
  2. the percentage of upper income households that were in Majority Upper Income Tracts.

Finally, Pew added these two percentages together and multiplied the sum by 100.  The result is a scale that ranges from 0 to 200: 0 means that no lower (or upper) income households in the city were located in majority lower income tracts (or, respectively, majority upper income tracts) while 200 means that every lower (and upper) income household in the city was located in a majority lower income tract (respectively, majority upper income tract).

It’s a complicated measure, which I will now simply call the segregation score, but I see its appeal. If it is unclear, the relevant point is that higher values of the measure imply that a randomly chosen lower or upper income household is more likely to have neighbors with similar household incomes.

Before continuing, note a couple of things:

  1. I like the measure in many ways (for example, it’s actually measuring something about households rather than only about neighborhoods). Of course, that does not mean I think it is the best way to measure segregation (income/economic or otherwise)—but I think there is no unambiguously “best” measure of this, as any such measure is an aggregation function.
  2. A higher score on this measure does not necessarily imply that a randomly chosen upper income household is likely to have fewer lower income neighbors. This is because the measure does not capture the full distribution of incomes in a number of ways.  As the point above alludes to, this is not something to fault the authors on.

2. Not Your Daddy’s Census Tract. The difficulty I want to describe is a matter of measurement.  The authors understandably want to talk about neighborhoods and spatial segregation.  Measuring neighborhoods is hard.  In particular, and as the authors describe (fn. 2),

The nation’s 73,000 census tracts are the best statistical proxy available from the Census Bureau to define neighborhoods. … As a general rule, a census tract conforms to what people typically think of as a neighborhood.

I agree wholeheartedly with the authors on this point.  However, defining a neighborhood at any one point in time is not the same as defining that neighborhood so that it is comparable across time.

Digression qua True Story. My mother’s family used to give directions with respect to a well-known “dirt pile” owned by their county.  Years passed and the dirt, well, went somewhere.  Around that time, her family started giving (and I think still gives) directions with respect to “where that dirt pile used to be.”

In a nutshell, the authors want to compare neighborhoods across about 30 years. In terms of their segregation measure described above, they need to choose a set of census tracts as the comparison set.  In particular, there are a few good reasons to choose a given set of census tracts and create the segregation measure for each city in 1980 and in 2010 using that same set of census tracts.

The definition of census tracts is described in this document. In a nutshell, census tracts are

…small, relatively permanent geographic entities within counties (or the statistical equivalents of counties) delineated by a committee of local data users. Generally, census tracts have between 2,500 and 8,000 residents and boundaries that follow visible features. When first established, census tracts are to be as homogeneous as possible with respect to population characteristics, economic status, and living conditions.

(Emphasis added.  And emphasized again in part.)

The highlighted part of this description indicates the difficulty.  In particular, the Pew analysis is quite (admirably) clear in their construction of the data: to compare the same neighborhoods between 1980 and 2010, they used census tracts from the 2000 census.  

Note: The authors had to choose between 2000 and 2010, as census tracts became universal only in the 2000 census.

So, what does this mean? Well, the census lines in question were drawn in 2000 with one of the goals being the maximization of homogeneity of economic status.  Thus, it is unsurprising that one finds greater economic homogeneity within census tracts between 2006 and 2010 than one finds in those same census tracts in 1980.  This is a convoluted version of “regression to the mean.”  In particular, if you create groupings so as to maximize some time-varying statistic (here, economic/income homogeneity), then many of the groupings will have (possibly very far) above average values of that statistic at the time of their creation.  Accordingly, they will tend to have lower levels of that statistic at any time other than when they are created.

Whew….put in the context of the segregation score analysis under discussion:

More economically homogeneous census tracts will generally lead to higher segregation scores as computed in the Pew report.

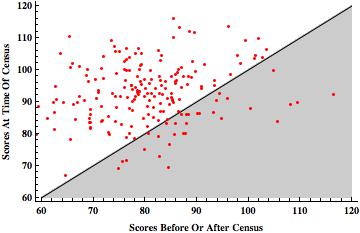
I programmed and ran a simple Monte Carlo experiment to demonstrate this.  I am happy to share the code and details with interested readers. (Simply email me.) In a nutshell, I ran 200 simulations and in 169 of them, the segregation scores from what the “census year” (i.e., when tracts were drawn) were higher than the same scores from the non-census year (i.e., when incomes vary but tracts do not). The results are displayed visually below.

One point that is key in thinking about the simulation results is that the income distributions in the two time periods were independently drawn.  This is unrealistic, but it presents most clearly and accurately the effect of the “regression to the mean” artifact introduced by the asymmetric timing of tract drawing.

[Visually, every dot in the white “upper left” part of the graph indicates a simulation where the score indicated increasing segregation, as found in the Pew report, and every dot in gray “lower right” part indicate the reverse.  Since the incomes are actually (by construction) unrelated in the simulations, one should expect—if the timing of the construction of census tracts doesn’t matter—that about half of the dots to be in each of the two areas.]

The main point here is more than that it is difficult to make an apples-to-apples comparison of neighborhoods over time—rather, from the “math of politics” angle, the key point is as follows:

The use of census tracts drawn in 2000 so as to accentuate intra-tract economic heterogeneity to compare income segregation in 1980 and the early 21st century biases the measure in favor of finding an increase in income segregation.

Before concluding, I want to make clear that I am not asserting (nor do I believe) that the conclusions of the Pew report are incorrect.  I am simply pointing out a difficulty with the construction of the data and, hence, the authors’ measure of change in segregation at a neighborhood level. Note that the difficulty I highlight would not apply if census tracts were drawn independently of the local distribution of economic statuses. Finally, it is also worth noting that the above-cited Census Bureau document points out the dilemma facing the Pew analysis:

The Census Bureau also requests that at the time each census tract is established, it contain (if possible) a population whose housing and socioeconomic characteristics are similar. Because the characteristics of neighborhoods and other small areas change with time, census tracts may become less homogeneous in succeeding censuses.

I guess an implication of my argument here is that the conclusion of the final sentence could be applied to preceding censuses as well.

In conclusion, I leave you with this.

Vitali Statistics: Measurability Issues in Education

Posted on by

This weekend, the Olympics drew our attention to those who leave everyone behind, leading us to question the nature of time itself (and I started thinking about algebra). So, I naturally began to think about measurement and education…

Recently, increased attention has been paid to the Obama Administration’s granting of waivers (or, “flexibility”) to states from the provisions of the No Child Left Behind Act of 2001 (NCLB).  The Act has been widely discussed since its passage at the beginning of the century, and I will focus only on one of its provisions (albeit arguably one of its most important).

CYA/Flame Retardant Provision. I am very aware acknowledge that these (both educational reform/performance in general and the NCLB in particular) are important, contentious, and complicated topics.  My point here is to illustrate a specific issue that I believe deserves some thought by those who are considering reform and/or reauthorization of NCLB.  

In a nutshell, NCLB requires states to develop standards by which their schools’ and school districts’ performances will be judged. I have a modest goal here: I will point out and try to explain a subtle but classic paradox hidden within one of the ways the NCLB calls upon states to measure educational success.

A key concept in NCLB is Adequate Yearly Progress (AYP).  This concept is measured at the school level for most elementary and high schools.  Without going into even more arcane details, it suffices to know that demonstrating achievement of AYP is desirable. I want to focus on what achieving AYP requires.

Specifically, in each year, tests are administered to students in reading, math, and science.  Waving at some details as we pass them by, success is essentially measured by the percentage of students passing each of these exams.  More importantly for our purposes, success rates must be measured in several ways.  For a given school, the success rates must be sufficiently high (and, generally, improving) in each of the following categories:

  1. all students,
  2. economically disadvantaged students,
  3. students from major racial and ethnic groups,
  4. students with disabilities, and
  5. students with limited English proficiency.
This design immediately raises the possibility of Simpson’s paradox, which can occur when comparing subpopulations with the population as a whole.  In this case, the relevant point is that an unambiguously improving school can still fail to satisfy AYP (and vice-versa).  Here is an example.
Suppose that a school has 100 students in both Years 1 and 2 and, for simplicity, consider only two “subgroups”: economically disadvantaged (“poor”) and not-economically-disadvantaged (“rich”) students.  Suppose that in Year 1, 20 of the school’s students were poor, and that 10 of these students “passed the exam,” whereas 72 of the 80 rich students passed the exam.  The school’s “scores” for Year 1 are then:
Poor: 10/20=50%.
Rich: 72/80=90%.
Total: 82/100=82%.

Now, in Year 2, suppose that 70 of the school’s students are poor, of whom 42 passed the exam, and all 30 of the rich students pass the exam. The school’s “scores” for Year 2 are then:

Poor: 42/70=60%.
Rich: 30/30=100%.
Total: 72/100=72%.
Uh oh. Viewed from a groups perspective, the school unambiguously improved its performance from Year 1 to Year 2 but viewed as a whole, the school’s performance has (similarly unambiguously) slipped.

The cause for the “paradox” is that the composition of the school changed between Years 1 and 2.  In year 2, the school gained students who had a lower success rate (even though, comparing apples to apples, this success rate increased) and lost students who had a higher (and also increased) success rate.  (Note that you can also construct this paradox only by altering the size of one of the groups.)

In a nutshell, it seems likely that the current construction of “Adequate Yearly Progress” might not measure what some of its proponents think it does.  Put another way, focusing on performance by subgroups (which is probably appropriate in this context and undoubtedly called for by the statute) immediately implies that this is an aggregation problem. Aggregation is a (or, perhaps, the) central question of political science.  But rather than get into that, I’ll simply leave you with this other formulation of Simpson’s paradox.
A Couple of Notes….
1. It should also be noted that others (e.g., Aldeman and Liu), have noticed a connection between Simpson’s paradox and educational testing, but I am unaware of anyone who has noticed the direct role of the paradox in the measurement of progress in the NCLB.
3. There are several other intriguing measurement aspects in both NCLB and the Obama Administration’s “Race to the Top” program.  Maybe I’ll write about them later.

But, Algebra is f(u)=n!

Posted on by

Putting real politics aside for a moment, I have a few comments on Andrew Hacker‘s op-ed in today’s New York Times, entitled “Is Algebra Necessary?” I will first answer his question.  Then I will discuss a few logical weaknesses of Hacker’s argument.

(In the interest of full disclosure, I am very proud to be a Unicorn, class of 1992.)

1. Wait, did you expect an answer?  Well, in a nutshell, the appropriate answer to Hacker’s tantalizingly ambiguous question is “yes and no.”  Clearly, algebra is not necessary for potty training, survival swimming, navel-gazing, or even fantasy football (though it helps). Strictly speaking, algebra is necessary for an admittedly much smaller set of life tasks.

The more important point is rejecting the false dichotomy put before us by Hacker.  Implicit in his piece is the presumption that something is either “necessary” or it is in need of serious, urgent reform.

The proper way to address whether algebra should be required is to ask what its mastery  does provide.  This is question of sufficient conditions.  In this case, one relevant conclusion is the fact that understanding algebra implies that one knows how to logically solve a problem.  Hacker might have a point (though it would require a lot more work than is evident in this piece) if he made a more measured argument that requiring algebra is too costly a means by which to ensure that high school graduates know how to logically solve a problem.  But his argument is not of that form.  Rather, he implicitly takes the position that “if something learned in a math class is not directly evident in everyday actions, it should not be required.”

Accordingly, Hacker has provided an argument against requiring that people learn about anything other than:

  1. sitting,
  2. Facebook,
  3. blogs,
  4. internet memes involving
    1. kitty cats
    2. Carly Rae Jepsen lyrics
    3. Queen Elizabeth,
  5. Amazon Prime,
  6. keyboard shortcuts, and
  7. Facebook.
  8. And Amazon Prime.

2. Oh, you meant “Is Unnecessary Algebra Necessary?”  Much of Hacker’s argument reminds me of this great correction. See, Hacker doesn’t want us to think that he thinks that we shouldn’t require, you know, useful math.

I’m not talking about quantitative skills, critical for informed citizenship and personal finance, but a very different ballgame…

Ummmm.  Okay, so the deal here is….what? Oh, yeah…Hacker wants to get rid only of the math that is not “critical for informed citizenship and personal finance.”  My brain hurts…perhaps because of all that math society made me take.  Exactly what are the bounds of “quantitative skills?”  This is never made precise, though apparently long division is a component.  As will become clear below, Hacker would have students learn how to understand where statistics and quantitative data come from and how they are constructed without having students learn about equations and fixed points.

For example, why is some data best described by the mean?  Why is it sometimes best described by the median?  What purpose does the mode serve?  What the hell is a variance?

Consider this interchange in the future.

Teacher: Suppose we flip a fair coin. If we let “Heads” equal 1 and “Tails” equal 0, the mean, or average, flip is equal to one-half.

Student: But, teacher, what does that mean? I’ve never seen a coin land on its edge.  

Teacher: Ahh, don’t you worry.  Andrew Hacker assures us that you don’t need to understand that.  Now shut up, go balance your checkbook, and vote.

In short, it doesn’t appear to me that Hacker has thought through one of the central  persuasive distinctions in his argument.  He frames it as a practical offering, but there’s very little practical guidance on how to decide what to keep and what to chuck from the curriculum.  On that note…

3. No, seriously, keep the important math. There may be another explanation, of course, but as far as I can make out, Hacker’s argument is either unintentionally incoherent or simply disingenuous insofar as he pretends to still have the cake he just ate.  For example, consider this snapshot of his stream of consciousness:

Being able to detect and identify ideology at work behind the numbers is of obvious use. Ours is fast becoming a statistical age, which raises the bar for informed citizenship. What is needed is not textbook formulas but greater understanding of where various numbers come from, and what they actually convey.

This makes no sense.  Let me rewrite this in sailing terms:

Being able to detect and identify the direction the ship is moving is of obvious use. Ours is fast becoming a seafaring age, which raises the bar for informed seamanship. What is needed is not concise summaries of how to sail a ship prepared by experienced sailors, but greater understanding of how various parts of the boat work, and how to actually work them.

4. I went to the bathroom and all I got was this lousy NYTimes Op-Ed. My final salvo is aimed at this passage:

What of the claim that mathematics sharpens our minds and makes us more intellectually adept as individuals and a citizen body? It’s true that mathematics requires mental exertion. But there’s no evidence that being able to prove (x^{2} + y^{2})^2 = (x^{2} - y^{2})^{2} + (2xy)^{2} leads to more credible political opinions or social analysis.

Notice the sleight of keyboard here: Hacker does not address the claim that mathematics sharpens our minds or makes us more intellectually adept.  Instead, Hacker asserts that there’s no evidence that knowing how to expand a quadratic equation leads to more credible political opinions or social analysis.

It is undoubtedly true that mathematics sharpens one’s mind and makes one more intellectually adept.  Indeed, it’s “so true” that one might challenge it as tautological.

In addition, and finally, Hacker’s claim that we should revisit the role of algebra and higher mathematics in the curriculum is based upon his assertion that there is no evidence that such training “leads to more credible political opinions or social analysis.”  Even if one grants Hacker’s concise summary of empirical evidence, this is still sleight of keyboard: neither of these conclusions is “necessary” for requiring algebra, at least no more so than it is for any other component of the curriculum.

As the world comes together to bash algebra and Michael Phelps, I leave you with this.

Regulatory ‘Rithmetic

Posted on by

A frequent talking point (e.g., like this) in this year’s presidential campaign is about the economic burden of federal regulations.  Given this focus, I thought it might be helpful to wade into the arithmetic behind this burden and the ways in which any president might alleviate it in the coming years.  I focus on the two points in turn.

Question 1: How Much Does Regulation Cost Us?

In general, policymaking through regulation has very small direct costs to taxpayers.  (For example, the total direct federal spending on regulatory agencies in 2012 is estimated to be just shy of $60 billion. To gain some perspective on this (it’s less than 2% of estimated total federal spending in 2012, see my post here.)   The beastly proportion of the burden, then, is through the various individual costs of compliance, foregone economic activity, and misallocation of resources.

Mitt Romney’s campaign has placed an emphasis on regulatory reform.  In fact, his campaign literature (linked above, page 3) states that regulations impose an annual cost burden of $1.75 trillion.

Digression.  The graphic used in the Romney policy brief compares the regulatory cost number with “all income taxes,” but omits payroll and Medicare taxes from this number.  While payroll taxes have an income ceiling (applies only to income up to a little more than than $110K/year), Medicare taxes do not and, more importantly, both are calculated as a percentage of earned income.  Total revenue from these two sources in 2012 is projected to be $779 billion.  Thus, since traditional income taxes and corporate income taxes are projected to total about $1.4 trillion, the total income tax burden is really in the neighborhood of $2.2 trillion.  This reality is indirectly implied, actually, by the source for the Romney’s numbers, a report commissioned by the Small Business Administration which states “…U.S. federal tax receipts, which equaled 21 percent of national income in 2008…” (p.6).

So, where does the astronomical figure of $1.75 trillion come from? As mentioned directly above, the number comes from a report by commissioned by the Small Business Administration and authored by Nicole V. Crain and W. Mark Crain, professors at Lafayette College. (Note: a critique of the methodology and lack of transparency in the Crain & Crain report is presented here. While one can always criticize an empirical study of anything with a scope such as that of the Crain & Crain report, it is safe to presume that federal regulations are in fact costly.  Accordingly, I am interested here only in the applicability of this number to the 2012 elections.)

Total Cost of Regulations

It is important to note at the beginning that the cost estimated by Crain & Crain is an estimate of total annual costs from federal regulations.  That’s a big point.  After all, as the report makes clear, the number includes costs from regulations that were promulgated (i.e., imposed) years and even decades before the current Administration took office.  At one level, who cares…right?  Romney’s campaign is running on a platform of shrinking government, regardless of where it was birthed.  On the other hand, Romney is running against Obama, and the policy piece linked to above directly proposes that a first step toward eliminating this burden is the repeal of various statutes and regulations passed during Obama’s administration.  Here are some quotes (pp.4-5):

  1. Repeal Obamacare. Mitt Romney has laid out a specific plan for dismantling Obamacare even without the congressional majorities required to strike it formally from the books…
  2. Reform Financial Regulation. As president, Mitt Romney will also seek to repeal Dodd-Frank and replace it with a streamlined regulatory framework…
  3. Reform Environmental Regulation. As president, Mitt Romney will eliminate the regulations promulgated in pursuit of the Obama administration’s costly and ineffective anti-carbon agenda…
  4. Review and Eliminate Obama-Era Regulations. One of the greatest problems with the federal bureaucracy is that each incoming presidential administration leaves in place much of what its predecessor constructed. The result is layer upon layer of often unnecessary or inconsistent regulation. Mitt Romney will not allow that practice to continue. On his first day in office, Romney will order all federal agencies to initiate repeal of any regulations issued by the Obama administration that unduly burden the economy or job creation. (Emphasis added.  You know, for emphasis.)

My point is that the Romney campaign is (quite understandably) pointing the anti-regulatory finger at the policies of Romney’s opponent, President Obama.  But, the cost referenced is by no means entirely attributable to his opponent’s policies, a point I return to  below.  Furthermore, if one looks at the source for his data about the annual costs of federal regulations, it is made clear (p.6) that the $1.75 trillion number is for 2008: “The findings in this report indicate that in 2008, U.S. federal government regulations cost an estimated $1.75 trillion…”

Digression. I personally find it odd, in light of the promise to circumvent Congress in “repealing” (or is it “dismantling”?) Obamacare and then to promise (p.5) “to restore a greater degree of congressional control over the agency rulemaking process. Our Constitution calls for our democratically elected Congress to make laws and for the democratically elected president to approve them.”
I will not even go into the arcane aspects of how it is hard (for me at least) to see how one can go beyond the Congressional Review Act in this regard without a dramatic reinterpretation/reversal of Supreme Court precedent established in INS v. Chadha.  Rather, I will simply note that the policy piece explicitly endorses both executive branch circumvention of Congress in pursuit of regulatory reform and promoting the legislative branch’s pride of place in the approval of federal regulations.

 

How Much Has the Cost Increased During the Obama Administration?

Another source of information for the Romney policy piece is the Heritage Foundation. (I think the piece they are referencing is this one, but I’m not sure.  Happy to be corrected, but I think that’s right, even though this is an updated version. To be clear, the two are very similar and I will clarify which one I am quoting from when needed: the earlier one will be called S11 (for Spring 2011) and the updated one will be referred to as F11.)  In the S11 report, the authors state on page 1:

Overall, the Obama Administration imposed 75 new major regulations from January 2009 to mid-FY 2011, with annual costs of $38 billion. There were only six major deregulatory actions during that time, with reported savings of just $1.5 billion.

Okay—to be clear, and comparing apples to apples with respect to the total cost figure of $1.75 trillion, this amounts to an increase in total regulatory costs since 2008 of about 2.2%.  In the F11 report, the authors state (again, on page 1): 

During the first three years of the Obama Administration, 106 new major federal regulations added more than $46 billion per year in new costs for Americans.

With this new data, the percentage increase in annual regulatory costs since 2008 is now a little under 2.7%.  To put this in historical perspective: according to Table 12 of the Crain & Crain report, the estimated per-household cost of federal regulation increased at an annual rate of slightly more than 2.8% between 2000 and 2004. (The Crain & Crain report suggests that its 2008 estimates are hard to compare to those for 2004, 2000, and 1995.  Accordingly, I’ll simply directed interested readers to take the time to look at Table 12 and think for a second about this disclaimer.)

Question 2: Which Regulations Are Costly, and Who is Responsible for Them?

Perhaps even more important for the presidential election than the total economic cost of regulations is the fact that the president is simply one actor in the regulatory drama. Regulations necessarily “fill in the blanks” for statutes passed by Congress.  Thus, it is important to consider where the new estimated costs are coming from in a statutory sense.  What laws are enabling/promoting costly regulation?

The F11 report describes the origins of the most costly regulations:

“The largest proportion of regulations by far stemmed from the 2010 Dodd–Frank financial regulation statute, which was responsible for 12 major rules increasing burdens in 2011, including six from the Securities and Exchange Commission, five from the Commodity Futures Trading Commission, and one from the Federal Reserve.”

Why is this relevant?  Regardless of one’s opinion about Dodd-Frank, it is important to note the following facts:

  • The SEC is an independent regulatory commission and, accordingly, beyond the scope of the president’s direct supervisory authority.
  • 3 of the 5 members of the SEC were appointed by George W. Bush.
  • Similarly, the CFTC is also an independent regulatory commission.
  • Also similarly, 3 of the 4 members of the CFTC were appointed by George W. Bush.
  • Finally, the Federal Reserve is an independent agency.

What this minutiae means in practical terms is that a president from either party has little to no control over these regulations.  Rather, Congressional action precipitated their promulgation and, barring a revision of our Constitutional understanding, similar action would be required to ensure these regulations are repealed.  In fact, this reality is acknowledged in Obama’s Executive Order 13579, which states that independent regulatory agencies

“should consider how best to promote retrospective analysis of rules that may be outmoded, ineffective, insufficient, or excessively burdensome, and to modify, streamline, expand, or repeal them in accordance with what has been learned. … each independent regulatory agency should develop and release to the public a plan, consistent with law and reflecting its resources and regulatory priorities and processes, under which the agency will periodically review its existing significant regulations to determine whether any such regulations should be modified, streamlined, expanded, or repealed so as to make the agency’s regulatory program more effective or less burdensome in achieving the regulatory objectives.” (Emphasis added.)

Regarding the point to which I am speaking (i.e., that the President’s direct authority over independent regulatory agencies is at best constitutionally circumspect), consider the closely related Executive Order 13563, which states that agencies

shall consider how best to promote retrospective analysis of rules that may be outmoded, ineffective, insufficient, or excessively burdensome, and to modify, streamline, expand, or repeal them in accordance with what has been learned. … each agency shall develop and submit to the Office of Information and Regulatory Affairs a preliminary plan, consistent with law and its resources and regulatory priorities, under which the agency will periodically review its existing significant regulations to determine whether any such regulations should be modified, streamlined, expanded, or repealed so as to make the agency’s regulatory program more effective or less burdensome in achieving the regulatory objectives. (Emphasis added.)

The differences between the two orders are minor in appearance, but important in effect.  First, the word “should” is conveying a mere suggestion (as opposed to “shall,” which is a polite command): the president has no authority to direct the internal affairs of an independent agency (this is one of the two principal implications of their independence). Second, executive agencies are, in congruence with previous practice dating back to President Reagan’s Executive Order 12291, directed to forward their plan for regulatory review to the Office of Information and Regulatory Affairs, which is located in the Office of Management and Budget, which (accurately) describes itself as follows:

The core mission of OMB is to serve the President of the United States in implementing his vision across the Executive Branch.  OMB is the largest component of the Executive Office of the President.  It reports directly to the President and helps a wide range of executive departments and agencies across the Federal Government to implement the commitments and priorities of the President.

Thus, the plan submitted by an executive agency is subject to explicit review by an agent of the president.  On the other hand, independent regulatory agencies are merely requested to release their plans “to the public.”

In conclusion, from a very real and long-standing point of the understanding of the separation of powers, the president essentially has no direct supervisory powers over the SEC, the CFTC, or the Federal Reserve. Rather, those who wish to stymie or reverse the regulatory efforts of these entities must look to Congress as well.

Conclusions, or “So what?” 

Federal regulation is a fact of life.  Even if one could contemplate a politically feasible way to eliminate massive swathes of existing regulations, good taste dictates that one should “dance with the one who brung ya.” In this case, that means that the total estimated cost should be compared with the total estimated benefits.  The points I have tried to make is that, relative to the 2012 election, there are two key points to consider:

  1. Even as presented by the Romney campaign, the expansion of the estimated costliness of federal regulations since 2009 has been modest, growing more slowly than during President George W. Bush’s first term.
  2. The president, regardless of party, lacks the authority to directly control the regulatory activity of the independent agencies responsible for the recent regulations estimated to be the most costly.
My goal in making these points is to focus the debate on the costs and benefits of specific regulations.  These are important policies and deserve to be discussed on the merits, as opposed to aggregate estimates that lack context.  With that in mind, I leave you with this.

 

Debits and Credits: Simple Budget Algebra

Posted on by

The US Federal Government faces a looming “fiscal cliff” as a result of current law calling for a simultaneous set of across-the-board cuts in spending and a rise in various tax rates.

There are many interesting aspects to this scenario, particularly given the divided partisan control of the two chambers of Congress.

Digression. Because Congress must send something to the President’s desk before he can sign it into law, this division is in some ways sufficient. The fact that this is an election year makes it even more interesting, as the collective impact of members’ electoral incentives in the House and Senate are quite different due to the overlapping electoral schedule in the Senate.  One final twist in this saga is the fact that this is the first election after the 2010 reapportionment of the House, meaning that a few members are running against each other and many more members are running for reelection in altered districts.  But much of that is a matter for discussion in a later post.)  

Today, I want to focus on a related question:

How might the federal budget be balanced without increasing revenues?

Before continuing, let me be clear:

  1. I am not arguing in favor of any particular solution (or even that an unbalanced budget is a problem that needs to be solved), but…
  2. I am arguing that balancing the budget without new revenues would require spending cuts that are either
    1. politically impossible (e.g., cutting Social Security without (permanently) cutting payroll taxes; slashing the defense budget),
    2. ridiculous (e.g., eliminating veterans’ benefits; shutting down the FBI), or
    3. both (e.g., eliminating Medicaid).

Digression. Yes, I do believe that the “Norquist Pledge” is incompatible with responsible government and/or the general maxim to not sign a pledge you don’t intend to uphold.

My purpose here is simply to provide a brief introduction to the budget and make the structure/composition of federal spending as clear as possible.  After all, it is not surprising that the federal budget is in some ways complicated and, after all, involve numbers that we rarely use and all rhyme with “Maximilian.”  What is a little surprising is that the federal budget can be described in fairly succinct terms that are also politically meaningful.

Note: All statistics reported here were drawn directly from the various historical tables/projections produced by the Office of Management and Budget. One could do the same thing using numbers from the Congressional Budget Office, too. I have no reason to believe that the differences would be particularly interesting.

Q. What is the size of the budget deficit?This is simultaneously a simple and complicated question.  First, for which year?  I will focus on the projected 2012 budget deficit.  Past budget numbers are obviously less desirable to use, and more distant projections are both (understandably) less reliable and (generally) partisan.  Second, “on-” or “off-budget?”  I will include “off-budget” items, too.  This is a judgment call, as this brings in most notably Social Security, which makes the corresponding budget deficit smaller.  (Precisely, federal trust funds are currently generating a surplus of a hair shy of $100 billion, which is about 7% of the total 2012 deficit. Oops, that gave it away.)

A. The 2012 budget deficit is $1.32 trillion. (The on-budget 2012 deficit is $1.42 trillion.)

Q. How much does the federal government spend?

A. With the caveats discussed above about the definition of the deficit, the federal government is projected to spend $3.8 trillion in 2012.  (Thus, revenues are projected to be $2.48 trillion.)

Q. What are the ten largest categories of spending?This, too, is a complicated question.  While a dollar is a dollar most days of the week, federal spending is famously not so simple.  Broadly speaking, spending comes in two forms: discretionary and non-discretionary.  Non-discretionary spending consists of two main components: “entitlements” and repayment of federal debt.  I will return to these distinctions below.  For now, let’s just treat a dollar as a dollar.

A. The ten largest categories of spending are (I’ll come back to the ones in quotes):

  1. Social security ($778 billion)
  2. Defense ($716 billion)
  3. “Income security” ($580 billion)
  4. Medicare ($484 billion)
  5. Health  ($362 billion) — This is mostly, but not entirely, Medicaid.
  6. Net interest ($225 billion)
  7. Education, Training, Employment, and Social Services ($139 billion)
  8. Veterans benefits and services ($130 billion)
  9. Transportation ($103 billion)
  10. Commerce and Housing Credit ($80 billion)It is useful to note that top top 3 categories account for over 50% of the federal government’s projected spending.  Furthermore, the top 2 categories are larger than the projected deficit.  

Q.What the heck is “Income Security,” and where can I get some?

A. The five largest individual subcategories in this category of federal spending are:

  1. Federal employee retirement and disability ($127 billion)
  2. Food and nutrition assistance ($113 billion)
  3. Unemployment compensation ($108 billion)
  4. Housing assistance ($60 billion)
  5. General retirement and disability insurance (NOT social security) ($8 billion)Thus, if you break these out individually, they would each rank no higher than 8th. As far as getting some of it, clearly the best way is to get a job with the federal government.

Q.What would I have to cut to balance the budget without increasing revenues?

A. Well, this is complicated—what’s fair game?  I will presume that net interest is off the table.  Similarly, though with less conviction, Social Security and Medicare are tough nuts to crack and, at least right now, the true impact of Social Security on the budget is small (regardless of whether positive or negative), unless one thinks that we could cut benefits without cutting the payroll taxes that are deposited into the Social Security trust fund.  First, consider how to answer the question without cutting defense spending (because, among other reasons, defense spending is a very complicated and variegated category).

These add up to about $2.2 trillion, or about 90% of projected 2012 revenues.
This plan leaves approximately $300 billion left to spend….and this is without funding veterans’ benefits, the FBI, federal prisons, the INS, or the federal courts…not to mention food stamps, highways, unemployment insurance, student loans….  In fact, there’s not enough even to fund Medicaid at its current levels.

A2. There’s no simple answer (or, rather, there are lots of simple answers—it’s just not clear what the “right one” is).  But reversing the logic makes clear what is not a very effective approach to balancing the budget: cutting discretionary domestic spending.  For example, suppose that the federal government simply and completely “got out of the business” of things like food assistance, unemployment insurance, pensions for federal employees, transportation projects like the interstate highway system, high speed rail, public transportation grants to state and local governments, higher education, research, and the like.  The total savings of these cuts?  Less than $600 billion. It’s a lot of money, to be sure, but that is less than 50% of the budget deficit.  In other words, even if the federal government eliminated all discretionary spending, we would still be running a deficit of over $700 billion.

In sum, if one believes that the most important priority for the federal government is to balance its budget (and, again, I do not think this should be the most priority to either conservatives or liberals), then you must also believe, as a corollary, that one or more of the following must be done:

  1. social security and/or medicare must be cut (without cutting payroll taxes commensurately),
  2. the defense budget must be slashed, and/or
  3. federal revenues must be raised.
(As a matter of constitutional fidelity and good taste, I withhold the option of defaulting on the debt.  It’s not nearly as effective a deficit cutter as some might think, anyway.  That’s why people still lend us money at interest rates essentially equal to zero.)

Hopefully I’ll find time in the near future to explain the structure of the revenue changes that have been proposed and/or might occur if we fall off the “fiscal cliff.”  In the meantime, I leave you with this.