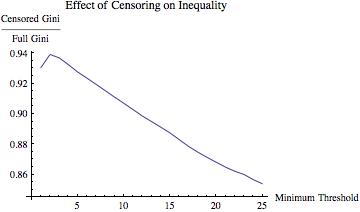
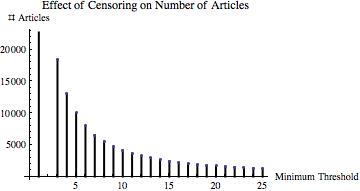
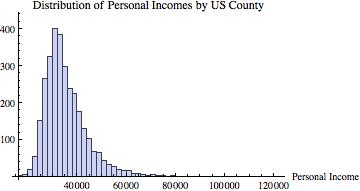
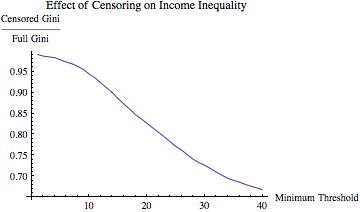
The IRS scandal, and in particular the handling (or, mishandling) of it by President Obama’s counsel, Kathryn Ruemmler, has raised a classic question: what did the President know, and when did he know it? In my mind at least, the question is predicated on the presumption that the president ought to know everything that is going on in the federal government.  After all, he is the administrator-in-chief, “the CEO,” the boss, the decider, the frickin’ POTUS!

A key point to remember through all such “management scandals” such as this is that the federal government is not a business, and particularly not the simplistic understanding of what “a business” is.  The reality is that the effectiveness of government can not be properly judged in an unambiguously unidimensional fashion like a classic (again, simplistic) business can be judged by its profits.  After all, one person’s “pork” is another’s “public purpose.”

That said, the real “mathofpolitics” point of this post is, even if the effectiveness of a government could be judged in a simple and uncontested unidimensional fashion, there are still situations in which the boss should not know everything that is going on.  Mind you, this is not a feasibility/constraints argument such as “the boss is simply too busy to worry about that).  Ironically, it is the opposite: there are situations in which the boss should not know some fact X precisely because the boss might care too much about X.  In other words, there are situations in which voters/shareholders (i.e., “principals”) might want their politicians/CEOs to not know something.  That is, the notion of plausible deniability is not exclusively a polite term for nefarious blame avoidance.

As I wrote a few days ago, political accountability is almost inherently an adverse selection problem. We as voters worry, and I think rightly, about the true motivations and goals of our representatives.  It is a little complicated, but consider the following simple situation to understand the importance of plausible deniability.

Suppose that a politician is charged with reviewing applications for grants.  Should the grant applications include the name of the applicants?  Well, practical concerns answer this in the affirmative: how else can you award grants if you don’t to whom to award them?

So, supposing the applications have the names on them, should the names be removed prior to the politician’s review of the applications?  That is, should the review be “blind” with respect to the applicants’ identities?  Before you answer, “yes, it’s only fair,” think why this is the case, because the reason is (at least) two-fold.  The more obvious of these two folds is based on the possibility that the politician is biased in favor (say) people who share his or her political views or partisanship.  (And let’s reasonably suppose that such favoring would be bad/inefficient relative to the goals of the grant program.)

In this scenario (the heart of the adverse selection worries alluded to above), removing the names creates a “more efficient” award process because it removes something that the awarding of the grants should not be conditioned upon from the ultimate determination of the awards.  This is a direct argument for “insulating” the politician from a piece of information about what’s going on in the government (i.e., who‘s getting grants?).

The second fold is more subtle.  Suppose that the politician is unbiased.  Technically, suppose that you almost certain that the politician is unbiased (i.e., the probability that the politician would exhibit favoritism is arbitrarily close to zero).  In simple probabilistic/expected utility terms, the argument sketched above would suggest that the gain from removing the names from the applications is also arbitrarily close to zero.  So, that argument would follow, you shouldn’t “pay much” or “go to much trouble” to remove the names from the applications, right?

Wrong. While this argument is correct “at the limit”—i.e., when the politician is absolutely, positively, without a doubt known to be unbiased—it falls apart (in game-theoretic terms, “unravels”) when there is even a scintilla of a (perceived) chance that the politician is biased.  The reason for this is that the politician, if he or she knows that the voters know that the politician can see the names, needs to worry about the voters inferring something (or “updating their beliefs”) about whether the politician is actually biased.  If he or she awards “too many” awards to his or her buddies (or, if we think there are a few friends, a few enemies, and a third group of non-friends/non-enemies, if the politician awards “too few” awards to his or her enemies), then a sophisticated voter will have increased (and perhaps greatly increased) reason to believe that the politician is actually biased.

The actual effect of this dynamic—for example, whether it will lead to too many or too few awards being awarded—depends on the parameters of the problem (specifically, the net benefit of an extra award and the weight that voters think a biased politician assigns to helping friends/hurting enemies), but the key to this second fold of the argument is as follows:

An unbiased politician will (ironically) condition his or her decisions on the names of the applicants if the politician is known/believed by the voters to have had the names when making his or her decisions.

So, when an advisor goes to great lengths to make it known (i.e., tells others, records the facts, etc.) that he or she did not tell the politician “the names,” this is not necessarily a “cover up.”  Rather, and particularly when the names are “politicized” (i.e., the awards are coming out in a biased way), this approach can be required (even if ultimately unsuccessful) to support a “de-politicized” decision process by the politician.

Another way to think of this is as follows: suppose that the politician chooses 10 awards, and the advisor, upon looking at the names in another room, realizes that the politician has given awards to 10 enemies.  At first blush, one might think—well, heck, if the politician is unbiased, then he or she could be told this fact.  But this is not true, because if this were a possibility, we (the voters) would (or should) wonder exactly whether the advisor told the politician that and the politician changed his or her mind/redid the awards whenever we see 10 of the politician’s friends receive awards.

Is this dynamic at play in the IRS scandal?  Yes.  It is at play throughout the federal government everyday.  For example, the idea of the special prosecutor (or special counsel) is entirely based on it.  Viewed from a strategic point, whether Obama should appoint a special counsel in this case is not unambiguous, as it could be akin to a Chamberlain moment vis-a-vis the House GOP, but I think I agree with Bill Keller that he should.

With that, I leave you with this.

American politics lately has been centered on SCANDAL! In particular, President Obama has been at the center of several well-publicized controversies, ranging from Benghazi to the IRS to the Department of Justice.

The politics of scandal is interesting.  For example, in none of the current scandals is there any real evidence that President Obama “did” anything directly (for example, as opposed to the crack-smoking scandal in Canada).  Rather, the questions center (appropriately) on whether the acts of subordinates reflect a general, if latent, policy/stance of the Obama Administration.  In all cases, the worry is essentially that the Obama administration is concerned with “political gain” at the expense of “good policy.”

Setting aside the difficulty of defining “good policy”—a ubiquitous problem that bedevils presidents from both parties—the “math of the politics of scandal” is similarly ubiquitous and bedeviling.  A potent view of the politics of scandal is provided by the notion of adverse selection. In particular, the adverse selection view of political scandals provides a useful understanding of why scandals are both inevitable and, more intriguingly, “important” even when the events directly associated with them are not necessarily so.

In a nutshell, adverse selection refers to situations in which there are multiple types of politicians (or any other agent), some of whom a given voter would prefer not to have in office, but the voter can not directly distinguish between the types.  Adverse selection is perhaps most visibly demonstrated in insurance markets: the insurance company would prefer to insure low risk individuals (e.g., good drivers), but provides a product that is necessarily particularly attractive to high risk individuals (bad drivers).

In the conventional view of politics, individuals who seek office are ambitious: campaigning is a costly and generally risky activity, and even holding office is not particularly remunerative. Accordingly, a degree of vanity or policy motivation is almost a sine qua non for a high profile political career.

Politicians who seek policy change are accordingly viewed with some suspicion: in order to secure public support for a new policy, a politician will seek to persuade voters that the policy is in their interest(s).  However, the costliness of campaigning, etc. and our belief that some politicians are accordingly driven by vanity or personal (rather than, or in addition to, “altruistic”) policy motivations implies that we view many such persuasion attempts with skepticism.  This is the first order effect of our awareness of the adverse selection problem: if there were no adverse selection problem, then we could rightly defer to the politician’s proposal.  (This protomodel can serve as a microfoundation for Richard Fenno’s famous “Home Style” argument: politicians seek to credibly emulate their constituents so as to ameliorate their constituents’ perceived likelihood of the adverse selection problem.)

The “politics of scandal” is a second order effect of adverse selection, in the sense that scandals, and the various courses they tend to run (e.g., slow burn, quick flame out, absolute barnburner, etc.) can be thought of as representing decentralized audits (or, perhaps, “sniff tests”) that politicians face from time to time.  If there were no adverse selection problem, a credible reform of consulate security would (or theoretically should) “end” the Benghazi scandal.  Similarly, if there were no adverse selection problem, replacing Michael Brown at FEMA would have quieted the backlash against President Bush following Hurricane Katrina.

So, what does the math of adverse selection tell us about scandal?  Well, the details of the model of course matter a lot, but a couple of generalizations are pretty robust.

1. Scandals will be prolonged when the politician is already suspected of being a “bad type” and, furthermore, the scandal will be prolonged by and promoted towards those voters who are already suspicious of the politician.  (Call it the Kanye effect?)
2. Admitting the failure and taking the blame for it can (will?) end the scandal.  This is because, under the typical adverse selection setting, the notion that the scandal is informative is precisely because the politician is actively trying to conceal his or her type. (Definitely call this the “Bay of Pigs/Janet Reno” effect.)
3. Scandals will be prolonged when the act(s) in question have a high probability of revealing new information about the politician.  That is, a scandal that strongly contradicts closely held beliefs of the politician’s supporters about the “true nature” of the politician (e.g., the AP subpoena scandal for Obama or the Rush Limbaugh prescription drug scandal) will be prolonged precisely because those opposed to the politician have a greater incentive to push, dig, and promote it.  To take the contrapositive, it is unclear that Obama would be (politically) harmed even if it came out that he personally audited and harangued tea party 501(c)(3) groups.  (Taking a similar example from the past, call this the “Dick Cheney’s Secret Task Force Effect.”)  (Also, as a mathofpolitics point, note that this is related to—in the sense of being the mathematical dual of—the “It Takes A Nixon To Go To China” class of signaling models.)
4. Scandals are more prolonged when it is more plausible that the politician knew about the problem before it happened.  Of course, the famous saying that It’s not the crime, it’s the cover-up seems to suggest otherwise.  In reality, the saying is making exactly this point.  The reason that the cover-up was so important (as, similarly though less spectacularly, was the Whitewater/Lewinsky impeachment fiasco with President Clinton) is that the cover-up activities, the obfuscating, the dodging are all consistent with a “bad type” reluctant to reveal this fact.

In the practical terms of the three aforementioned Obama imbroglios, these generalities suggest to me the following rough-and-ready-and-completely-seat-of-the-pants ranking of their “seriousness” from least to most serious:

1. (Least) Benghazi,
2. IRS,
3. (Most) AP subpoenas.

This post is already arguably too long, but I’ll quickly list the empirical characteristics that helped me make this list in light of the four generalities above:

1. Attorney General Holder is still in office and presumably a close confidante of President Obama.  Note that Attorneys General are Ground Zero for modern Cabinet-level scandals. (Sorry, Department of the Interior, the heydays of the 19th and early 20th Century are currently no more but, that said, never forget the now-disemboweled Marine Mineral Service and the Deepwater Horizon disaster.)
2. The AP scandal is arguably distinctly “unDemocratic”—particularly in light of its obvious analogies with the various Nixon scandals (also applies to the IRS scandal even more directly, though the IRS was significantly reformed after Nixon’s fiascos).
3. It’s not clear how Obama can come out “against” the AP scandal (for example, see this).  This is a bit complicated, but it is thin needle to thread to be against the AP scandal and against potentially-national-security-compromising leaks of classified information.

So, Obama rightly has his work cut out for him.  If it were me, which it most definitely ain’t, I don’t know what I’d do.  Probably obfuscate, wait for the public to become disinterested in subpoenas and journalists, and pray for a happy, healthy, and well-covered royal birth.

With that, I leave you with this.

As a theorist, I write models.  (There is a distinction between “types” of theorists in political science.  It is casually and superficially descriptive: all theorists write models, just in different languages.)

One of the biggest complaints I hear—from both (some) fellow theorists and (at least self-described) “non-theorists”—is the following equivalent complaint in different terms:

1. Theorists: …but, is your model robust to the following [insert foil here]
2. “Non-theorists”:  …but, your model doesn’t explain [insert phenomenon here]

It is an important point—perhaps the most (or, only) important point—of this post that these are the same objection. I have been busy for the past month or so, and in the interest of getting those phone lines lit up, I thought I would opine briefly on what a social science model “should” do.  Of course, your mileage may vary, and widely.  This is simply one person’s take on an ages-old but, to me at least, underappreciated problem.

Models necessarily establish existence results. That is, a model tells you why something might happen.  It does not even purport to tell you why something did, or will, or did not, or will not, happen.  (Though I have a different take on a related but distinct question about why equilibrium multiplicity does not doom the predictive power of game theory.)

Put it another way: a model is a (hopefully) transparent, complete (i.e., “rigorous”) story or narrative offering one—most definitively not necessarily exclusive—explanation for one or more phenomena.  I regularly (co-)write models of politics (recent examples include this piece on cabinets and other things, this piece on the design of hierarchical organizations, this piece on electoral campaigns, and this forthcoming book on legitimate political decision-making).  All of them are “simply” arguments.  None of them are dispositive.  The truth is, reality is complicated.

Politics is a lot like meteorology.  We all know and enjoy, repeatedly, jokes along the lines of “hell, if I could get a job where you only need to be right 25% of the time….,” but the joke makes a point about models in general.  Asking any model of politics to predict even half of the cases that come to you after reading the model is like asking the meteorologist to, say, correctly and exactly predict the high and low temperature every day at your house.  No model does that.  Furthermore, it is arguable that no model should be expected to, perhaps, but that’s a different question.  More importantly, no model is designed to do this…because it defeats the point of models.

Running with this, consider for a moment that a lot more is spent on meteorological models than political, social and economic ones (e.g., the National Weather Service budget is just shy of $1 billion and that of the Social and Economic Sciences at the NSF is approximately 10% of that). Models are best when they are clear and reliable.  Sometimes, reliability means—very ironically—“incomplete in most instances.”  Consider a very reliable “business model”:

“Buy low, sell high.”

This model, setting aside some signaling, tax, and other ancillary motivations (which I return to below), IS UNDOUBTEDLY THE BEST MODEL OF HOW TO GET RICH. 

However, it is incomplete.  WHAT IS LOW? And you can’t answer, “anything less than `high,'” because that merely pushes the question back to WHAT IS HIGH?

Of course, some people will rightly say that this indeterminacy is what separates theory from praxis.  The fact is, even the best good models don’t necessarily give you “the answer.”  Rather, they give you an answer.  One can reasonably argue, of course that a model is “better” the more often its basic insights apply.  But that is a different matter.

Returning to the “buy low, sell high” model, consider the following quick “thought experiment.”  Suppose that Tony Soprano approaches you and says, “please buy my 100 shares in pets.com for $10,000.”  Should you?  According to the model, the answer is clearly no: shares in pets.com are worth nothing—and never will be worth anything—on the “open market.”

But, running with this, Tony has approached you for “a favor.”  Let’s not be obtuse: he bailed you out of that, ahem, “incident” in Atlantic City back in ’09, and you actually have two choices now: pay $10,000 for worthless shares in pets.com or have both of your kneecaps broken. (Protip: buy the shares.)

The right choice, given my judicious/cherry-picking framing, is to buy shares high and “sell them low.”  Well, this proves the model wrong, right?  No.

It simply change the definition of “value when sold.”  It reveals the incompleteness of the theory/model.

This is basically my point: no model is truly “robust,” even to imaginable variations and, conversely, it is certainly the case that smart people like you can come up with examples that at least seem to suggest that the model doesn’t describe the world.

It’s kind of an analogy to a foundation of empirics and statistics: central tendency.  Models should indicate an interesting part of a phenomena of interest.  In this sense, a good model is an existence proof, sort of like the Cantor Set: it demonstrates that things can happen, not necessarily that they do.  The fact that those things don’t always happen doesn’t really say much about the model, just like you read/watch the weather every day even while making those jokes about the meteorologist.

And with that seeming non sequitur, I push forward and leave you with this.

The idea of a “permission structure” has attracted some attention this week.  The basic idea of this phrase, it seems, is as follows: A doesn’t trust B to do some activity X because A fears that B does not have A’s best interests at heart in the “realm” of X.

A good example of this type of distrust is when you get in a car accident.  Both you and your car insurance company are faced with the difficulty of who should determine what “should be fixed” under your policy. You don’t want the insurance company to determine this, because they have an incentive to minimize costs and, accordingly, denote too few things as “needing to be fixed.”  On the flip side, your insurance company doesn’t want to let YOU determine this, because suddenly that “three martini lunch bumper ding” you got 6 months ago is deemed “covered” and repaired on the insurance company’s dime.

The point I want to make is that, at least in a very specific sense, permission structures can (almost) never solve the problem they are purportedly designed to solve.  In a nutshell, think of a simple model where there are two types of politicians: one type is “faithful” and the other type is “biased.” To continue to keep it simple, suppose that the faithful type of politician will always use (say) increased taxes in a way that benefits you and the biased type will use them in such a way as you would rightly prefer not to have your taxes increased for how he or she would spend the resulting revenues.

The idea of a permission structure is to clarify to you, the voter, when the politician is a faithful type and not a biased type.  As Obama said recently,

We’re going to try to do everything we can to create a permission structure for [Congressional Republicans] to be able to do what’s going to be best for the country.

The impossibility of “creating a permission structure” (regardless of whether it is through “third party authentication” or otherwise) is due to the use of the term “creating” (it is also doubly ironic for Obama to announce that he and his team are going to “try to do everything we can” to create one).  The math of politics of this post is a remarkably simple point that seems to have been closely brushed by many of the analysts, and it rests on the concept of “creating” such a structure. Suppose that a third-party authenticator could be found/created/cajoled—or even simply brought to everyone’s attention—that would lead voters to say “hey, cool—you’re the faithful type!”  Then think for a minute and ask yourself—why would the biased type not find/create/cajole such an authenticator?  Indeed, in many (but not all) situations, the biased type would have a stronger incentive to create a permission structure than the faithful type.

There’s always the possibility that when the politician is a biased type no such authenticator could be found/created/cajoled.  But, let’s be honest, that’s a pretty knife-edge case.  (I mean, have you heard of Wayne LaPierre?)  Also, it’s at least theoretically possible that the biased type is relatively uninterested in raising your taxes (and, accordingly, little interest in creating a permission structure).  I leave this to the side, as such a presumption describes exactly zero American voters’ beliefs about politicians.

Accordingly, the problem with Obama’s statement wasn’t the elitist/wonkish sound of the term, or the possibility that it strengthened a perception of him being unwilling to “knock some heads” or otherwise “lead.”  (Nonetheless, I do appreciate the irony of conservatives banging on the table saying “WHY DON’T YOU LEAD LIKE THE GUY WHO CREATED MEDICAID AND GOT BOTH THE CIVIL RIGHTS & VOTING RIGHTS ACTS PASSED!!!”)

…No, the only real problem with the statement is that Obama pointed out the man behind the curtain: many voters can’t trust “government” right now precisely because they have a strong suspicion that government is trying to fool them.  This is very sad to me for many (nonpartisan) reasons, but it illuminates the adage:

Never trust a man who says, “Trust me.”

With that, I leave you with this.

In light of this week’s horrific series of events in Boston, I (and many others) have been thinking a lot about what exactly the “Miranda warning”—or more specifically, “being Mirandized”—means.  There are a lot of angles to this, and I will focus on only one. In the interest of full disclosure, I believe that the bar should be set incredibly high for the state, and I support Mirandizing individuals in all circumstances.  (Furthermore, I believe this because I believe that the state properly possesses police powers.  But that’s a different post.)

[Note. Thanks to John Kastellec for very helpfully pointing out that this is actually a current issue before the Court (in another case).  The NYTimes has an editorial on the issue, too. ]

So, much debate has occurred about whether one possesses the “Miranda rights” prior to being Mirandized.  My understanding is that the rights described in the warning are always possessed, and so I will assume this in what follows.  This is not only because I believe this to be the case, but also because assuming otherwise makes the strategic implications of giving or not giving the warning much more powerful and concomitantly less interesting.

Of course, as many have said, it is hard to imagine that anyone does not know their Miranda rights given the fame of the case and the warning’s high profile usage on crime drama shows.  On the other hand, some have pointed out that in times of high stress, individuals do crazy things and/or forget well-known ones.

That said, I want to focus on a potential importance of the issuance of the Miranda warning as a focal point.  It provides a focal point for all people, many of whom may or may not be sure of their ultimate legal liability, to “pool” by shutting/”lawyering” up.  Summarizing the argument below, the “Miranda warning” is equivalent to a publicly known signal of “we’re about to question you with intent to convict you.”  According to this argument, the warning’s importance is not for the defendant in question, but rather for the non-defendants of the future. (This sets aside another very cogent argument that Miranda warnings help remind the police themselves to mind their p’s and q’s, a social good in multiple ways.)

The basic idea of my unraveling argument is this: suppose that every question the police ask you has a probability p>0 of making you recognize some fact that, for simplicity, will implicate you with probability q>0.  (We all have this positive probability, right?)*

If p=1, then Miranda makes no difference.  However, for most/all people, p<1.  Now, suppose that police just start questioning.  Furthermore, suppose that everybody follows the following strategy: answer questions until you suspect that the question might be self-incriminating.  Should you follow that strategy, too?  Be honest until you fear that you shouldn’t answer that question?

Uh-oh.  What should the police infer when you stop answering questions?  Well, obviously they should infer that something in that question they just asked suggested some fact that you believe might incriminate you in a crime/legal quandry.  So, you should stop answering earlier than this point. Of course, you have to do this before “the question in question,” so a simple line of thought points out that, if everyone plays the “answer as long as it seems safe” strategy, YOU should just refuse to answer any questions even before they are asked.

Taken at face value, that “unraveling argument” suggests that Miranda is unnecessary.  Everybody should just lawyer up.  But…we don’t (or shouldn’t) like that world: nobody ever cooperates with police, regardless of p<1 and q>0.  That is, even if the police were asking me innocently if I saw the school bus drive past my house earlier than usual today, I should most definitely stop them at “did you see…” with a “TALK TO MY LAWYER.”

Instead, we would prefer a world that, for sufficiently small q—i.e., worlds where we are very very unlikely to have done anything wrong, people can answer the police’s questions without fear.

THAT’S WHAT MIRANDA DOES: IT TELLS YOU WHEN YOU MIGHT BE IN TROUBLE.  The essence of Miranda is that the police can use spontaneous confessions, etc., but if they bring you into custody and interrogate you with the idea of getting information with which to potentially convict you, they must give you the warning first.  Think of this, for simplicity, as the court saying to police: “if YOU think that q is pretty high—high enough to warrant putting an individual into custody and interrogating them—then you have to offer them the opportunity to stop the questioning before it begins.”

The unraveling argument suggests why, while it might or might not be important to give the Miranda warning per se to Dzhokhar Tsarnaev, it is arguably very important that they at least be required to tell them that they are not giving him the warning.  That is, they notified the people of “the public safety exception.”  They should notify him as well.

Note, even more importantly, that this is not a “defendant-based” civil liberties argument.  That is, this is not about protecting Tsarnaev from self-incrimination.  Rather, it is an argument that, if the police don’t have to do this, then police will be less effective at protecting us because we will all have reason to always decline to answer questions in future situations.

________________________________

A side note here: though the 5th Amendment protects one against self-incriminating testimony on the stand, it does not protect you against the police from using your taking the 5th Amendment as a signal as to what/where they should investigate.  In other words (as I understand it), the 5th Amendment is applicable only if the facts at hand would actually incriminate oneself, and therefore is truly applicable only if you actually did something for which you might be punished (or have good reason to believe so).  This is a big difference than Miranda rights, which are ex ante, rather than ex post, rights accorded to all citizens regardless of their legal liability.

The debate about gun control provides a great example of a collision between political issues and public policies. As I describe more below, most “political issues” are labels/shortcuts for describing preferences about multiple specific government policies/laws. The point of this post is that gun control, a political issue, is like a cookie.  How I feel about cookies is not necessarily well-linked with how I feel about the various ingredients in a cookie. For example, I am strongly “pro-cookie.” However, while I am “pro” butter, eggs, and chocolate, I am strongly opposed to vanilla extract, baking soda, and flour.

This culinary digression is actually illustrative of an important point for those who are upset following yesterday’s vote on the Manchin-Toomey background checks amendment.  In particular, while I have already argued that the vote is not necessarily indicative of a failure of democratic institutions,* the point I want to make, and the “math of politics”of this post, is that political issues represent convenient and way to discuss attitudes and goals, but they are very rarely neatly mapped onto, and generally subsume multiple, public policies.

Another way to think of it is that many (but not all) political issues collapse various public policies into something like a “less strict/more strict” dimension.  “Gun control,” “environmental regulation,” and “consumer safety” are each examples of this.

People can respond very differently to the policies that compose a political issue than they do to the issue itself.  Sometimes in paradoxical ways.

The implications of this for the gun control debate are clearly illustrated by first considering the various questions and poll results about public policies in this Pew survey:

Support for Various Gun Policies

And then considering the more general “bundled” question about the political issue reported in this AP-GfK poll.  This poll (conducted this week) asked just over 1000 Americans “Should gun laws in the United States be made more strict, less strict or remain as they are?”  In response to this deceptively straightforward question,

• 49% responded “be made more strict,”
• 38% responded “remain as they are,” and
• 10% responded “be made less strict.”

(You can find a very convenient tally of similar polls here.)  To be clear and slightly provocative, this kind of public support actually makes the Senate look a little aggressive on gun control: 54 Senators out of 100 voted in favor of the Manchin-Toomey background checks amendment (really 55, counting Reid’s “procedural nay” vote as a “yea”).

This is one basis of what social scientists refer to as “framing.”  Incumbents end up running against strategic challengers, and issues like gun control are a potential nightmare.  Accepting for the sake of argument that there is and will remain overwhelming public support for expanded background checks, every Senator cast a tough vote yesterday. (Hell, Reid cast TWO tough votes—ask John Kerry how to explain this kind of thing.  Oh wait, don’t.)  In the words of challengers-to-be, each Senator was either “against expanded background checks” or “for stricter gun laws,” neither of which is a clear electoral winner.  On the other hand, in the words of every Senator-about-to-seek-reelection, he or she was either “for expanded background checks” or “protecting gun rights,” both of which have pretty strong public support, especially on a state-by-state basis (as this excellent Monkey Cage post makes very clear).

As a final (non-strategic) “math of politics” point, before one thinks that this tension between public support on a given issue and public support for the issue’s constituent policies challenges democratic competence, note that this is all easily understood as an implication of Arrow’s theorem or an instantiation of the referendum paradox or the Ostrogorski paradox.

Yeah, I mentioned Arrow’s Theorem again, so I leave you with this.

_________________________________________________________

* Relatedly, I most fervently disagree with the argument that the Senate is antidemocratic. The Senate is explicitly not designed to deliver “one-person-one-vote” representation.  Furthermore, the founders really meant it.  But I’ve been told that political behavior has far broader appeal than political institutions.

Yesterday, the Senate—in line with expectations—rejected the most basic of gun control proposals.  In light of the Newtown massacre—an event that shook all of us—this might seem shocking.  For example, even leaving aside the emotional pull that perhaps we can as a nation call that horrible day back and make it right, the proposal arguably had/has 90% support among the public.

Does this demonstrate a problem with the Senate or, perhaps, democracy itself? Simply put, no.

Let me be clear: I have many family and friends who own and use guns for hunting and sport, and I do not believe that the debate about “taking away guns” is worth the breath or typing it takes to describe such a practically ludicrous concept. However, in the interest of full disclosure, I do not own a gun, and do not think that a gun is appropriate to keep in my house. Okay…that said…now I’m going to blow your mind. WITH SOCIAL SCIENCE.

First, the Senate ain’t done.  I’ll just note that and then spare you (for now) yet another installment of my “votes matter for signaling to constituents” argument (which would imply we might see the background checks come in through another, presumably bundled, amendment).

Second, and the “math of politics” part of this post, this vote demonstrates the not-so-gentle implications of the subtle interaction of psychology, indirect democracy, and multi-issue politics.

Before I continue, let me apologize for my shortcuts, I am about to unfairly but succinctly imply that gun rights advocates are all gun owners.  This supposition is demonstrably false in the general context, of course, because plenty of people cheer for teams representing colleges that they not only didn’t attend, but couldn’t have if they wanted to.  (You know who I’m talking about, right?)  That said, here we go…

A realist/game theoretic interpretation of democracy implies that it “works” (if it does) only because voters hold incumbents accountable for their decisions.  Taking this logic on its own and pairing it with the overwhelming empirical support for background checks, the intuitive conclusion is that democracy must be failing: clearly a few Senators at least must be ignoring the demands of their constituents.  Right? (Don’t worry, I’m not about to make an argument based on the (mal)apportionment of the Senate or sampling error.)

Umm, yes, perhaps…until you realize that Senate elections choose Senators, not positions. Once you realize this, you “think down the game tree” a bit as an incumbent and you think…

“Well, I vote on lots of different issues.  Each voter comes into the voting booth and does something like a weighted sum over the various positions I am seen as favorable/reliable on and then compares me with the challenger.”

In a nutshell, this means that every incumbent—when faced with a vote on any issue—considers the weight (or, in the terminology of political science, salience) of that issue with his or her electorate. (I’m abstracting from individual-voter-level differences for simplicity.)

Thus, the impact of an incumbent’s gun control vote on any given voter i‘s “approval/support” for the incumbent is basically something like

,

where is the importance of gun control (larger values imply gun control is more important to i) and is “+1” if i agrees with the incumbent’s vote on gun control and “-1” otherwise.

Note that this is just one issue among many.  The total approval/support of the voter for the incumbent is something like

.

Okay, that’s voting.  Now let’s think about psychology. In a nutshell, who cares most strongly about background checks? This is sort of a Olsonian–Tversky&Kahneman effect:

Those who encounter the policy most often care the most about it.

Gun owners (or people who think/fear they might want to buy a gun someday) will generally have (or be believed by incumbents to have) larger values of . And, to cut to the chase, many of them will not prefer to submit to (say) background checks.  (After all, most these voters are, indeed, good Americans.)

So, while 90% of the voters might prefer a vote for background checks (i.e., for a vote for yesterday’s amendment), few if any of them assign nearly as large a value of as the 10% of the voters who oppose background checks.

This matters because an incumbent—in the spirit of democratic responsiveness—is responsive to a voter on any given single issue only to the degree that the voter’s vote is responsive to the incumbent’s vote/stance on that issue. Congress deals with many issues. For better or worse, my argument here is that “gun control/gun rights” votes are generally more important/dispositive for voters who refer to the issue as “gun rights.”

Here’s a picture suggesting this, from Pew:

Revealed Differential Importance of Gun Rights/Control

In spite of that picture, note that, according to my argument, this is not about polarization in the classical sense (the two sides don’t necessarily have wildly different policy goals). While gun control is a fairly partisan issue, it is not actually a strongly partisan one. Rather, background checks represent an issue that (in line with the Olson shout-out above) present “concentrated costs” to an arguably much-less-than-majority group and “dispersed benefits” to a larger-than-majority group. If we had a referendum on the background checks amendment (and everybody had to turnout and vote), then I have no doubt that the Manchin-Toomey amendment would win in a landslide. But that’s not the way indirect democracy works. (And, for another day, thank goodness for that. AMIRITE, CALIFORNIANS WITH SCHOOL-AGE CHILDREN?)

So, I am sad that our nation tears and blows itself apart over both the issue and its instantiation. I cried (a lot) watching the coverage of Newtown and for a few days afterwards. That said, the institutional and psychological/preference realities of the issue mean that at least I sleep well at night confident in the notion that this strife does not imply anything untoward about our politicians or voters. To put it another way, as hard as it is to accept sometimes, democracy is about choices—the logic above is a convoluted (but more precise) way of saying “pro-gun rights voters will “throw the bum out” for a pro-gun-control vote…and a pro-gun-control voter probably won’t do the same to his or her incumbent for a pro-gun-rights vote.” As I disclosed above, I am more than happy to be proven wrong on this in 2014. And with that, I put my money where my mouth is and leave you with this.

________________________________________________________________________

PS.  According to this article, Sen. Toomey (R-PA) “argued that `the Second Amendment does not apply equally to every single American…'”  I can’t resist the opportunity to suggest that this is wrong headed on arguably two counts.  First, it is distinctly poor taste and shortsighted to get into an Orwellian “some people have more rights than others” interpretation of the Constitution. Second, and more controversially, the Second Amendment is actually a guarantee of a collective (read: State) right, rather than an individual one.  I mean, one is the loneliest number even for militias?  (Also, are “poor taste” and “shortsightedness” synonymous in equilibrium?)

[This is an installment in my irregular series of articles on the minutiae of what I do, “Inside Baseball.”]

Lately I have been working on a couple of models with various signaling aspects.  It has led me to think a lot more about both “testing models” and common knowledge of beliefs.  Specifically, a central question in game theoretic models is: “what should one player believe when he or she sees another player do something unexpected?” (“Something unexpected,” here, means “something that I originally believed that the other player would never do.”)

This is a well-known issue in game theory, referred to as “off-the-equilibrium-path beliefs,” or more simply as “off-the-path beliefs.” A practical example from academia is “Professor X never writes nice letters of recommendation.  But candidate/applicant Y got a really nice letter from Professor X.”

A lot of people, in my experience, infer that candidate/applicant Y is probably REALLY good. But, from a (Bayesian) game theory perspective, this otherwise sensible inference is not necessarily warranted:

By supposition, Prof. X never writes good letters, so

.

Houston, we have a problem.

From this perspective, there are two questions that have been nagging me.

1. How do we test models that depend on this aspect of strategic interaction?
2. Should we require that everybody have shared beliefs in such situations?

The first question is the focus of this post. (I might return to the second question in a future post, and note that both questions are related to a point I discussed earlier in this “column.”)  Note that this question is very important for social science. For example, the general idea of a principal (legislators, voters, police, auditors) monitoring one or more agents (bureaucrats, politicians, bystanders, corporate boards) generally depends on off-the-path beliefs. Without specifying such beliefs for the principal—and the agents’ beliefs about these beliefs—it is impossible to dictate/predict/prescribe what agents should do. (There are several dimensions here, but I want to try and stay focused.)

Think about it this way: an agent assigning zero-probability to an action in these situations, if the action is interesting in the sense of being potentially valuable for the agent if the principal’s beliefs after taking the action were of a certain form, is based on the agent’s beliefs about the principal’s beliefs about the agent in a situation that the principal believes will never happen. Note that this is doubly interesting because, without any ambiguity, the principal’s beliefs and the agent’s beliefs about these beliefs are causal.

Now, I think that any way of “testing” this causal mechanism—the principal’s beliefs about the agent following an action that the principal believes the agent will never take—necessarily calls into question the mechanism itself.  Put another way, the mechanism is epistemological in nature, and thus the principal’s beliefs in (say) an experimental setting where the agent’s action could be induced by the experimenter somehow should necessarily incorporate the (true) possibility that the experimenter (randomly) induced/forced the agent to take the action.

So what?  Well, two questions immediately emerge: how should the principal (in the lab) treat the “deviation” by the agent?  That’s for another post someday, perhaps.  The second question is whether the agent knows that the principal knows that the agent might be induced/forced to take the action. If so, then game theory predicts that the experimental protocol can actually induce the agent to take the action in a “second-order” sense.

Why is this? Well, consider a game in which one player, A, is asked to either keep a cookie or give the cookie to a second player, B. Following this choice, B then decides whether to reward A with a lollipop or throw the lollipop in the trash (B can not eat the lollipop).  Suppose also for simplicity that everybody likes lollipops better than cookies and everybody likes cookies better than nothing, but A might be one of two types: the type who likes cookies a little bit, but likes lollipops a lot more (t=Sharer), and the type who likes cookies just a little bit less than lollipops (t=Greedy).  Also for simplicity, suppose that each type is equally likely:

.

Then, suppose that B likes to give lollipops to sharing types (t=Sharer) and is indifferent about giving lollipops to greedy types (t=Greedy).

From B’s perspective, the optimal equilibrium in this “pure” game involves

1. Player B’s beliefs and strategy:
   1. B believing that player A is Greedy if A does not share, and throwing the lollipop away (at no subjective loss to A), and
   2. B believing that A is equally likely to be a Sharer or Greedy if A does share, and giving A the lollipop (because this results in a net expected gain for B).
2. A’s strategy:
   1. Regardless of type, A gives B the cookie, because this (and only this) gets A the lollipop, which is better than the cookie (given B’s strategy, there is no way for A to get both the cookie and lollipop).

Now, suppose that the experimenter involuntarily and randomly (independently of A’s type) forces A to keep the cookie (say) 5% of the time.  At first blush, this seems (to me at least) a reasonable way to “test” this model.  But, if the experimental treatment is known to B and A knows that B knows this, and so forth, then the above strategy-belief profile is no longer an equilibrium of the new game (even when altered to allow for the 5% involuntary deviations). In particular, if the players were playing the above profile, then B should believe that any deviation is equally likely to have been forced upon a Sharer as a Greedy player A.  Thus, B will receive a positive expected payoff from giving the lollipop to any deviator.  Following this logic just about two more steps, all perfect Bayesian equilibria of this “experimentally-induced” game is

1. Player B’s beliefs and strategy:
   1. B believes that player A is equally likely to be a Sharer or Greedy if A does not share, and thus giving A the lollipop
   2. It doesn’t matter what B’s beliefs are, or what B does if A does share. (Thus, there is technically a continuum of equilibria.)
2. A’s strategy:
   1. Regardless of type, A keeps the cookie, because this gets A both the cookie and lollipop).

By the way, this logic has been used in theoretical models for quite some time (dating back at least to 1982).  So, anyway, maybe I’m missing something, but I am starting to wonder if there is an impossibility theorem in here.

President Obama proposed his 2014 budget this week.  A huge document, it contains a number of interesting policy proposals.  One that is attracting a lot of attention concerns the “chained CPI.” In a nutshell, this change will reduce the rate of growth in social security payments over the next decade.  Overall, the proposal arguably represents a compromise with Congressional Republicans.  Perhaps understandably (although this is a classic chicken-egg situation), some Congressional Democrats and liberal interest groups are outraged. Did Obama overreach?  Has he sold out his party? To both questions, I argue “no,” and I also assert that, while Obama may be a pragmatist, this proposal isn’t a fair-minded compromise with the GOP.  It’s far more aggressive than that and positioned for the 2014 elections.

From a strategic standpoint, Obama is in an interesting situation.  He’s a lame duck president with a receding mandate and an approaching midterm election.  I think he has policy/legacy motivations to drive him to do more in his second term than most (all?) two-term presidents.  Accomplishing this would be greatly assisted by the Democrats doing well in the 2014 midterm elections.  (And, of course, he might want such a thing either on partisan or personal grounds, too.)

Going into 2014, the Democrats are in a tough situation in the Senate and a long-shot in the House. So how does Obama’s proposal affect this?  Not much in the grand sense, of course, because budget proposals are “inside baseball” for the most part and it seems unlikely (to me at least) that the public will buy into the narrative that “Obama is attacking Seniors.”

However, Obama’s proposal puts the House GOP in a bind and, by extension, potentially presents Senators of both parties with a challenge.  On the one hand, the House GOP can not simply “sign off” on Obama’s budget: for one, it raises taxes and, two, it’s Obama’s budget.  In taking a stand against his budget, though, the House GOP must come up with a reason.  While Boehner can try to claim that the proposal is incremental and doesn’t go far enough with respect to entitlement reform, this approach forces the GOP to come up with an even more aggressive plan or keep pushing the Ryan plan. Given the public’s lack of support for cutting social security, and the fact that Social Security is technically “off budget” and therefore of little value in reducing the budget deficit in the short term, it’s not clear to me what the GOP can counter with in terms of spending.  (And, of course, I wrote about this last year: there’s almost no way to balance the budget without new revenues or dramatically shrinking the defense budget.)

One way to view this is that Obama has “caved” to GOP demands and that this is another example of Obama not realizing that Congressional Republicans can not be dealt with.  Somewhat ironically, Obama’s very public and tangible concessions (even if “incremental”) are arguably the strongest positive bargaining move he has made in recent years. The key words here, and the “math of politics” of this post, are public and tangible.  By going public with a specific proposal, Obama is framing the next stage of the budget process. He is putting the spotlight on the Republicans and thereby calling their bluff that they have a politically feasible budget plan. (It’s a dual version of the logic I sketched out during Boehner’s stratagem during the fiscal cliff showdown.)

It is important to note that Obama’s budget was two months late.  He waited until after sequestration hit, after the House and Senate each passed their own budget resolutions.  In a colloquial sense, this forces the House GOP to respond to his proposal, as opposed to the Senate’s.

By going public (as opposed to privately bargaining with Boehner), Obama imposes “audience costs” on both himself and the House GOP.  For Obama, he would face a potentially huge cost if his budget was approved and sent to his desk for his signature.  (This isn’t going to happen, but a partial version could.) For the House GOP, of course, it now has the public’s attention on their budget priorities again.  That hasn’t worked out so well in the past.

By being tangible (i.e., by including the specific, headline garnering proposal regarding Social Security), Obama has arguably placed himself as the compromiser.  More importantly, Obama’s proposal presents Congressional Democrats with a useful foil and “clear indicator” of the importance of the 2014 elections.  Key here from Obama’s perspective is that he’s a lame duck president: if he has policy goals, he can be less concerned with maintaining his short-term popularity.  He can also turn to his partisan base and say (truthfully, in my opinion): “if you want Democratic priorities to win, you need to give me—and you—a Democratic House.  More importantly, perhaps, you better be darned sure the Democrats hold onto the Senate.”

With that, I think of the President of the Senate, and leave you with this.

I have been thinking a lot lately about this very interesting post by Kristina Lerman.  The post is excellent: succinct and well-written, data-centric, and relevant beyond the data’s idiosyncratic qualities.  In a nutshell, Lerman’s central question is whether the rate of information production is outstripping the rate at which we (choose to or can) consume and digest it.

Of course, information overload is clearly an important problem for scholars and practitioners alike (and, accordingly, not one with any obvious and easy answer). But upon reflection, I am still wondering whether it is a problem at all.  Given my second-mover advantage, I will cherry-pick one of the arguments in the post.

In a section titled “Rising Inequality,” Lerman uses the Gini coefficient of citations to physics papers as a measure of scholarly inequality.  Since the Gini coefficient has grown over the past 6 decades, Lerman concludes that “a shrinking fraction of papers is getting all the citations.”  This is undoubtedly true once one slightly rewords it as “a shrinking fraction of the papers made available is getting all the citations.”  This is an important qualifier, in my opinion, and the central point of this post.

Any notion of inequality is inherently relative. As I read it, Lerman’s argument is that the increase in information production has potentially caused us to use cues or heuristics to manage the decision of what information we as scholars consume.  Lerman argues that this is bad because the Gini coefficient has increased along with the rate of publication, indicating that the cues and heuristics we are employing is narrowing our attention to a smaller set of articles and creating a “rich get richer” dynamic in terms of citations and scholarly focus.

However, is this conclusion warranted by the data?  I am not so sure: the Gini coefficient, like any measure of inequality, is potentially sensitive in counterintuitive ways to the set of things being compared to one another.

The nature of Gini coefficients. Lerman’s argument that higher Gini coefficients are bad is very sensible if one thinks that the “pie” of citations is fixed in size and/or that the low citation articles are somehow “unjustly” receiving fewer citations.  At least in my opinion, neither of these suppositions is reasonable in this context.  There’s a number of ways to skin this cat, but I think this is the easiest.  Suppose, for the sake of argument, that the number of citations an article will receive is independent of the number of articles uploaded (or, accepted into an APS journal).  Then, suppose that only those articles that will receive m citations are uploaded.  As the costs of uploading/writing/publishing decrease, m would presumably decrease as well.  With this in hand, the key question is:

Holding the latent population of articles fixed, how does the Gini coefficient of the uploaded articles change as m increases?

Note that decreasing m increases the number of articles uploaded.  To me, at least, Lerman’s implicit argument is that decreasing m “should” decrease inequality (i.e., decrease the Gini coefficient).

This isn’t necessarily the case.  I ran a simulation to demonstrate this with a very large set of “pseudo-data.”  Specifically, I generated 100,000 observations from a Pareto(k=1,=1.35) distribution.  This pseudo-data yielded a Gini coefficient of .  Then I truncated the distribution at various values of m and computed the ratio of the Gini coefficient of the resulting truncated data set and the Gini coefficient of the full data set. If decreasing m “should” decrease inequality, then this ratio should be increasing in m.

The results are displayed below

The simulated data demonstrate that increasing the selectivity of the upload/publication process can actually decrease inequality among the (changing set of) uploaded/published papers.  In other words, increasing the rate of uploading/publication of articles can increase inequality without reference to information overload or any changes in citation behavior. 

Out of curiosity, I went out and got some real data. For simplicity, I downloaded the per capita personal incomes of each US county for 2011 (available here).  This data looks like this:

I then did an analogous analysis, varying the income threshold from $20,500 to $40,000, computing the ratio of the Gini of the truncated data to the Gini of the overall data set at each increment of $500.  The results of this are below.

Again, as one gets more “elite” with respect to the inclusion of a county in terms of income into the calculation of the Gini coefficient, estimated inequality decreases.

Now, it is probably very simple to find examples in which the opposite conclusion holds.  But that’s not the point: I am not arguing that Lerman is wrong.  Rather, I am making a point about inequality measurement in general.  In line with my earlier point about Simpson’s paradox and education policy, comparing relative performance between different sets-even nested ones-is tricky.*

Also, as an aside before concluding, it occurred to me that the data used by Lerman seems to vary from point to point.  While the data demonstrating the rapid increase in production rate over the past two decades is from arxiv.org (and, further, note this graph, which is a more “apples-to-apples” comparison), the data on which the Gini coefficients are calculated are papers “published in the journals of the American Physical Society.”  These are two very different outlets, of course: arxiv.org is not peer-reviewed, while the journals of the American Physical Society are.

While I do not have the data that Lerman is working from in her post, the difference between the two data sources might be important due to changes in the number & nature of publication outlets over the time period.

Specifically, consider either or both of the following two possibilities:

1. Presumably, there are publication outlets other than the APS journals.  If this is the case, even if the APS journals have published a fixed and constant number of papers per year, changing publication patterns could be far more important in determining the Gini coefficient of citations to articles published APS journals than the overall article production rate.
2. After doing some poking around, I came across this candidate as the likely source of Lerman’s data for the Gini coefficient calculations.  I may be wrong, of course, but if this is the data used, it considers only intra-APS journal citations.  If this is the case, then one is not really looking at inequality of attention/citations broadly—just inequality within APS articles.  The sorting critique from the above point applies here, too.

Conclusion: Comparisons of Inequality Are Not Always Comparable. Again, I really like Lerman’s post: this is a hard and important question.  My point is only that measuring inequality, a classic aggregation/social choice problem, is inherently tricky.

With that, I leave you with this.

____________________________

* As another aside, it occurs to me that these issues are intimately related to some common misunderstandings of Ken Arrow’s independence of irrelevant alternatives axiom from social choice.  But I will leave that for another post.